of a line?" width="1057" height="600" />Here we will learn about the equation of a line, including recognising the gradient and y-intercept of a straight line, and finding the equation of a line from a graph.
There are also worksheets on the equation of a line based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
The equation of a line is the algebraic representation of a line using cartesian coordinates.
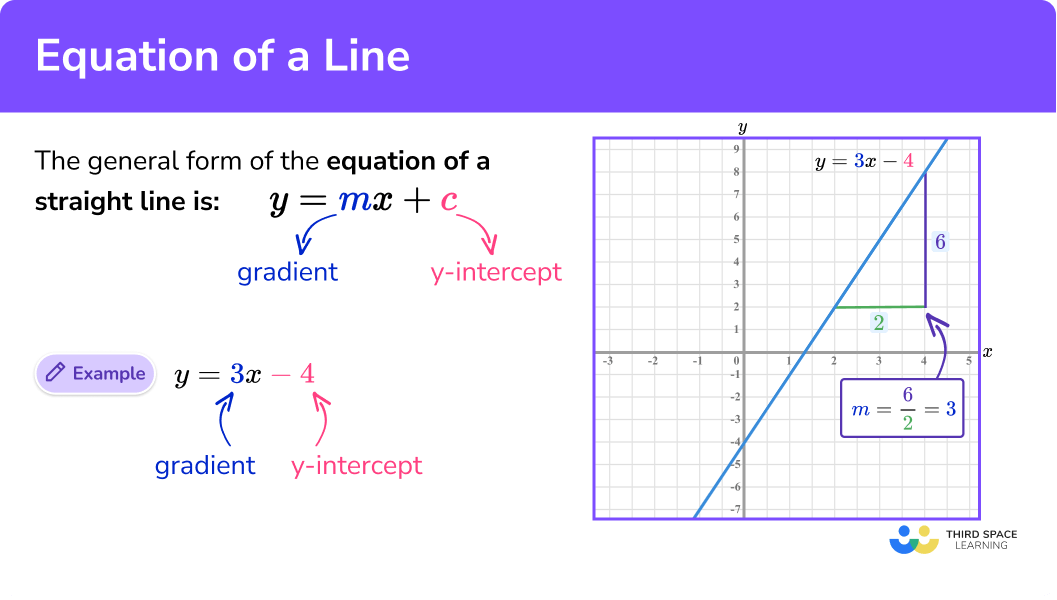
The general form of the equation of a straight line is written as y = mx + c .
Where m is the gradient of the straight line
and c is the y -intercept of the straight line.
The coordinate ( x,y ) lies on the line y = mx + c giving us a linear relationship between x and y . The term linear equation is given to any straight line.
E.g.
Let’s look at the line y = 3x − 4 .
Here, we can find any y -coordinate given the value for x by substituting into the equation y = 3x − 4 .
\begin &y=3 \times 1-4 \\\\ &y=3-4 \\\\ &y=-1 \end
So when the x value is 1 and the y value is -1 , this gives us the coordinate ( 1, -1 ) which lies on the line as shown below.
Not all straight lines will appear to be exactly in the form y = mx + c so we need to understand how we determine the gradient (or steepness of the line) m , and the y -intercept (the point where the line intersects the y -axis) c from equations that are not in the form y = mx + c .
Here are some examples of linear equations not in the form y = mx + c
In order to easily determine m and c we need to rearrange the equation to make y the subject.
E.g.
Take the equation above of y + 17 = 6x and make y the subject.
By rearranging the equation into the form y = mx + c we can clearly state that the gradient m = 6 and the y -intercept c = −17 .
From this, we can draw the straight line onto a set of axes.
of a line?" width="1057" height="600" />
In order to find the equation of a straight line:
of a line" width="1057" height="599" />
of a line worksheet" width="788" height="261" />
of a line worksheet" width="788" height="261" />
Get your free equation of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
of a line worksheet" width="788" height="261" />
of a line worksheet" width="788" height="261" />
Get your free equation of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Equation of a line is part of our series of lessons to support revision on straight line graphs. You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Work out the equation of the straight line given in the diagram below.
Two points that lie on the line are: ( 0, 4 ) and ( 2, 8 ).The line passes through these two given points.
So the gradient
2 State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
3 Write the equation of the line in the form y = mx + c .
As the slope m = 2 and y intercept c = 4 ,
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 1, −4 ) and ( 3, 2 ).
So the gradient
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Write the equation of the line in the form y=mx+c .
As m = 3 and c = −7, y = 3x − 7
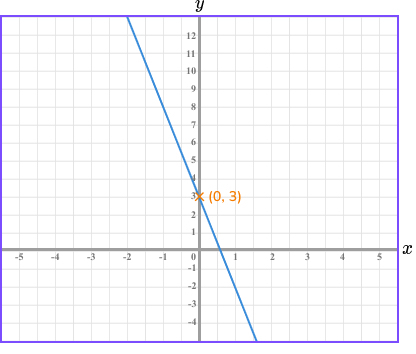
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 1, −2 ) and ( −1, 8 ).
So the gradient
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
of a line example 3 step 2 1" width="416" height="354" />
Write the equation of the line in the form y=mx+c .
As m = −5 and c = 3, y = −5x + 3
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( −3, −2 ) and ( 2, −7 ).
So the gradient
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Write the equation of the line in the form y=mx+c .
As m = −1 and c = −5, y = −x − 5
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 4, 10 ) and ( −2, 7 ).
So the gradient
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Write the equation of the line in the form y=mx+c .
As m = \frac and c = 8, \;y = \fracx + 8
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( −2, −4 ) and ( 2, −5 ).
So the gradient
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Here, c = -4.5 or c=-\frac .
Write the equation of the line in the form y=mx+c .
The coefficient of x is the gradient m and the constant term is the y -intercept c . If the coefficient of x is 1 , remember this is written as x only as 1x = x .
Ignoring the negative values in a coordinate means that the gradient will be calculated incorrectly. When picking two coordinates, make sure that the coordinates go through the corner of a grid square. If there are negative values, make sure you use them with the negative symbol.
When calculating the gradient of a straight line, be careful to not mix up the coordinates.
E.g.
Looking back at example 5 , we have the two points that lie on the line being ( 1, −2 ) and ( −1,8 ).
The change in y could be correctly calculated as 8 \; − \; −2 but the change in x is then incorrectly calculated as 1 \; − \; −1 . This would result in the gradient of the line being 5 and not −5 .
Avoid counting squares to work out the change in x or y . Use the axes scales or label the coordinates, then find the difference between them.
A common error is to not calculate the gradient of the line.
Let’s look at example 1 ,
A error could be made by identifying the y -intercept and determining that the equation of the line is y = x + 4 .
This will only work when x = 0 but not for any other value for x .
